一、圖的定義

圖是一種比樹更復(fù)雜的一種數(shù)據(jù)結(jié)構(gòu)，在圖結(jié)構(gòu)中，結(jié)點之間的關(guān)系是任意的，任意兩個元素之間都可能相關(guān)，因此，它的應(yīng)用極廣。圖中的數(shù)據(jù)元素通常被稱為頂點 ( V e r t e x ) (Vertex) (Vertex)， V V V是頂點的有窮非空集合， V R VR VR是兩個頂點之間的關(guān)系的集合(可以為空)，可以表示為圖 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}。

二、相關(guān)術(shù)語

2.1 無向圖

給定圖 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}，若該圖中每條邊都是沒有方向的，則稱其為無向圖 ( U n d i g r a p h ) (Undigraph) (Undigraph)。對圖 G G G中頂點 v v v和頂點 w w w的關(guān)系，可用無序?qū)?( v , w ) (v,w) (v,w)表示，它是連接 v v v和 w w w的一條邊 ( E d g e ) (Edge) (Edge)。

2.2 有向圖

給定圖 G = { V , { A } } G=\{V,\{A\}\} G={V,{A}}，若該圖中每條邊都是有方向的，則稱其為有向圖 ( D i g r a p h ) (Digraph) (Digraph)。對圖 G G G中頂點 v v v和頂點 w w w的關(guān)系，可用有序?qū)? v , w > v,w> v,w>表示，它是從 v v v到 w w w的一條弧 ( A r c ) (Arc) (Arc)，其中 v v v被稱為弧尾 ( T a i l ) (Tail) (Tail)， w w w被稱為弧頭 ( H e a d ) (Head) (Head)。

  弧尾也叫初始點 ( I n i t i a l (Initial (Initial N o d e ) Node) Node)，弧頭也叫終端點 ( T e r m i n a l (Terminal (Terminal N o d e ) Node) Node)。

2.3 完全圖

對于任一無向圖，若其頂點的總數(shù)目為 n n n，邊的總數(shù)目為 e = n ( n − 1 ) 2 e=\frac {n(n-1)} {2} e=2n(n−1)​，則稱其為完全圖 ( C o m p l e t e d (Completed (Completed G r a p h ) Graph) Graph)。

2.4 有向完全圖

對于任一有向圖，若其頂點的總數(shù)目為 n n n，邊的總數(shù)目為 e = n ( n − 1 ) e=n(n-1) e=n(n−1)，則稱其為有向完全圖。

2.5 稀疏圖和稠密圖

對于具有 n n n個頂點， e e e條邊或弧的圖來說，若 e e e很小，比如 e n log ⁡ n en\log n enlogn，則稱其為稀疏圖 ( S p a r s e (Sparse (Sparse G r a p h ) Graph) Graph)，反之稱其為稠密圖 ( D e n s e (Dense (Dense G r a p h ) Graph) Graph)。

2.6 權(quán)和網(wǎng)

賦予圖中邊或弧的數(shù)值稱為權(quán) ( W e i g h t ) (Weight) (Weight)，它可以表示從一個頂點到另一個頂點的距離；帶權(quán)的圖稱為網(wǎng) ( N e t w o r k ) (Network) (Network)。

2.7 稀疏網(wǎng)和稠密網(wǎng)

帶權(quán)的稀疏圖、稠密圖稱為稀疏網(wǎng)、稠密網(wǎng)。

2.8 子圖

對于圖 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}和圖 G ′ = { V ′ , { E ′ } } G'=\{V',\{E'\}\} G′={V′,{E′}}，若 V ′ ⊆ V V'\subseteq V V′⊆V且 E ′ ⊆ E E'\subseteq E E′⊆E，則稱 G ′ G' G′為 G G G的子圖 ( S u b g r a p h ) (Subgraph) (Subgraph)。

2.9 鄰接點

對于無向圖 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}，若 v ∈ V v\in V v∈V、 w ∈ V w\in V w∈V且 ( v , w ) ∈ E (v,w)\in E (v,w)∈E，則稱頂點 v v v和頂點 w w w互為鄰接點 ( A d j a c e n t ) (Adjacent) (Adjacent)，并稱邊 ( v , w ) (v,w) (v,w)依附 ( I n c i d e n t ) (Incident) (Incident)于頂點 v v v和頂點 w w w，或稱邊 ( v , w ) (v,w) (v,w)與頂點 v v v和頂點 w w w相關(guān)聯(lián)。

對于有向圖 G = { V , { A } } G=\{V,\{A\}\} G={V,{A}}，若 v ∈ V v\in V v∈V、 w ∈ V w\in V w∈V且 v , w > ∈ A v,w>\in A v,w>∈A，則稱頂點 v v v鄰接到頂點 w w w，頂點 w w w鄰接自頂點 v v v，并稱弧 v , w > v,w> v,w>與頂點 v v v和頂點 w w w相關(guān)聯(lián)。

2.10 度、入度與出度

在無向圖中，頂點 v v v的度 ( D e g r e e ) (Degree) (Degree)等于與該頂點相關(guān)聯(lián)的邊的數(shù)目，記為 T D ( v ) TD(v) TD(v)。

在有向圖中，頂點 v v v的度等于該頂點的入度與出度之和，記為 T D ( v ) = I D ( v ) + O D ( v ) TD(v)=ID(v)+OD(v) TD(v)=ID(v)+OD(v)，其中頂點 v v v的入度 ( I n D e g r e e ) (InDegree) (InDegree)為以該頂點為弧頭的弧的數(shù)目，記為 I D ( v ) ID(v) ID(v)，頂點 v v v的出度 ( O u t D e g r e e ) (OutDegree) (OutDegree)為以該頂點為弧尾的弧的數(shù)目，記為 O D ( v ) OD(v) OD(v)。

2.11 路徑、簡單路徑與路徑長度

路徑 ( P a t h ) (Path) (Path)是任意兩個有關(guān)聯(lián)的頂點之間的邊或弧，在圖 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}中，頂點 v 1 v_1 v1​到頂點 v n v_n vn​的路徑是一個頂點序列 ( v 1 , v 2 , … , v i , v j , … , v n ) (v_1,v_2,\dots,v_i,v_j,\dots,v_n) (v1​,v2​,…,vi​,vj​,…,vn​)，對于上述序列中的任意相鄰的頂點 v i v_i vi​和 v j v_j vj​，若圖 G G G是無向圖，則有 ( v , w ) ∈ E (v,w)\in E (v,w)∈E，若圖 G G G是有向圖，則有 v , w > ∈ A v,w>\in A v,w>∈A。

對于給定的一條路徑，若該路徑對應(yīng)的序列中的頂點不重復(fù)，則稱為該路徑為簡單路徑。

路徑上邊或弧的數(shù)目稱為路徑長度。

2.12 回路與簡單回路

若某一路徑中的第一個頂點和最后一個頂點相同，則稱該路徑為回路，也稱為環(huán) ( C y c l e ) (Cycle) (Cycle)。

在某一回路中，若除去第一個頂點和最后一個頂點外，其余頂點均不重復(fù)，則稱為該回路為簡單回路，也稱為簡單環(huán)。

2.13 連通圖與連通分量

在無向圖中，若從頂點 v v v到頂點 w w w有路徑，則稱為 v v v到 w w w是連通的，若該圖中的任意兩個頂點間都是連通的，則稱該圖為連通圖 ( C o n n e c t e d (Connected (Connected G r a p h ) Graph) Graph)。無向圖中的極大連通子圖稱為連通分量 ( C o n n e c t e d (Connected (Connected C o m p o n e n t ) Component) Component)。這里的極大就是盡可能地包含更多的頂點。

2.14 強連通圖與強連通分量

在有向圖中，若從頂點 v v v到頂點 w w w有路徑，從頂點 w w w到頂點 v v v也有路徑，則稱為 v v v和 w w w是強連通的，若該圖中的任意兩個頂點間都是強連通的，則稱該圖為強連通圖。有向圖中的極大連通子圖稱為強連通分量。

2.15 生成樹、最小生成樹與生成森林

具有 n n n個頂點的連通圖的極小連通子圖稱為生成樹，生成樹包含這一連通圖的 n n n個頂點和 n − 1 n-1 n−1條邊。這里的極小是盡可能少地包含邊。

通常把各邊帶權(quán)的連通圖稱為連通網(wǎng)，在連通網(wǎng)的所有生成樹中，對每一棵生成樹的各邊權(quán)值求和，其中權(quán)值最小的生成樹稱為該連通網(wǎng)的最小生成樹。

非連通圖的各連通分量的生成樹組成的森林稱為生成森林。

3. 圖的性質(zhì)

3.1 性質(zhì)1

若圖中有 n n n個頂點 v 1 , v 2 , … , v n v_1,v_2,\dots,v_n v1​,v2​,…,vn​， e e e條邊或弧，其中頂點的度分別為 T D ( v 1 ) , T D ( v 2 ) , … , T D ( v n ) TD(v_1),TD(v_2),\dots,TD(v_n) TD(v1​),TD(v2​),…,TD(vn​)，則有
e = 1 2 ∑ i = 1 n T D ( v i ) e=\frac {1} {2} \sum_{i=1} ^ {n} TD(v_i) e=21​i=1∑n​TD(vi​)

3.2 性質(zhì)2

一棵有 n n n個頂點的生成樹有且僅有 n − 1 n-1 n−1條邊。

4. 圖的存儲結(jié)構(gòu)

4.1 鄰接矩陣

用于無向圖、有向圖

在存儲含有 n n n個結(jié)點的圖 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}時，將圖中的所有頂點存儲在長度為 n n n的一維數(shù)組中，將圖中邊或弧的信息存儲在 n × n n\times n n×n的二維數(shù)組中，我們稱這個二維的數(shù)組為鄰接矩陣。假設(shè)圖 G G G中頂點 v v v和頂點 w w w在一維數(shù)組中的下標(biāo)分別為 i i i、 j j j，則該圖對應(yīng)各鄰接矩陣定義如下：

若該圖為無向圖或有向圖，則
A r c s [ j ] [ j ] = { 1 , ( v , w ) ∈ E 或 v , w > ∈ A 0 , 其 他 Arcs[j][j]=\begin{cases} 1, (v,w)\in E或v,w>\in A\\ \\ 0, 其他 \end{cases} Arcs[j][j]=⎩⎪⎨⎪⎧​1,0,​(v,w)∈E或v,w>∈A其他​  若該圖為無向網(wǎng)或有向網(wǎng)，則
A r c s [ j ] [ j ] = { w i j , ( v , w ) ∈ E 或 v , w > ∈ A ∞ , 其 他 Arcs[j][j]=\begin{cases} w_{ij}, (v,w)\in E或v,w>\in A\\ \\ \infty, 其他 \end{cases} Arcs[j][j]=⎩⎪⎨⎪⎧​wij​,∞,​(v,w)∈E或v,w>∈A其他​  其中， w i j w_{ij} wij​為邊或弧對應(yīng)的權(quán)值。

定義圖中的頂點：

class VertexMatrix(object):
    """
    圖的一個頂點
    """
    def __init__(self, data):
        self.data = data
        self.info = None

定義圖：

class GraphMatrix(object):
    """
    圖的鄰接矩陣
    """
    def __init__(self, kind):
        # 圖的類型: 無向圖, 有向圖, 無向網(wǎng), 有向網(wǎng)
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 頂點表
        self.vertexs = []
        # 邊表, 即鄰接矩陣, 是個二維的
        self.arcs = []
        # 當(dāng)前頂點數(shù)
        self.vexnum = 0
        # 當(dāng)前邊(弧)數(shù)
        self.arcnum = 0

無向圖及其鄰接矩陣、有向網(wǎng)及其鄰接矩陣如下：
A r c s = [ 0 1 0 1 1 0 0 1 0 0 0 1 1 1 1 0 ] A r c s = [ ∞ 1 2 ∞ ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ ∞ ∞ ] Arcs=\begin{bmatrix} 0 1 0 1 \\ 1 0 0 1 \\ 0 0 0 1 \\ 1 1 1 0 \end{bmatrix} Arcs=\begin{bmatrix} \infty 1 2 \infty \\ \infty \infty 3 \infty \\ \infty \infty \infty 4 \\ \infty \infty \infty \infty \end{bmatrix} Arcs=⎣⎢⎢⎡​0101​1001​0001​1110​⎦⎥⎥⎤​Arcs=⎣⎢⎢⎡​∞∞∞∞​1∞∞∞​23∞∞​∞∞4∞​⎦⎥⎥⎤

​

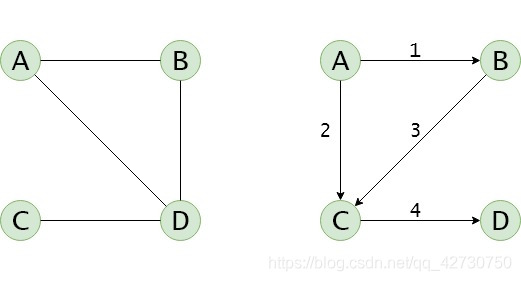
鄰接矩陣的特點如下：

(1) 由于在創(chuàng)建鄰接矩陣時，輸入頂點的順序不同，其相應(yīng)的鄰接矩陣也是不同的；

(2) 對于含有 n n n個頂點的圖，其鄰接矩陣一定是 n × n n\times n n×n的二維數(shù)組；

(3) 無向圖的鄰接矩陣具有對稱性，可采用壓縮存儲的方式存儲；

(4) 對于無向圖，若某一頂點 v v v在一維數(shù)組中的下標(biāo)為 i i i，則該頂點的度為鄰接矩陣的第 i + 1 i+1 i+1行中值為1的元素的總數(shù)目；

(5) 對于有向圖，若某一頂點 v v v在一維數(shù)組中的下標(biāo)為 i i i，則該頂點的出度為鄰接矩陣的第 i + 1 i+1 i+1行中值為1的元素的總數(shù)目，入度為鄰接矩陣的第 i + 1 i+1 i+1列中值為1的元素的總數(shù)目。

構(gòu)造一個具有 n n n個頂點 e e e條邊的無向網(wǎng)的時間復(fù)雜度為 O ( n 2 + n e ) O(n^2+ne) O(n2+ne)，其中對鄰接矩陣的初始化使用了 O ( n 2 ) O(n^2) O(n2)的時間。

4.2 鄰接表

用于無向圖、有向圖

使用鄰接表存儲圖時，將圖分為兩個部分：

第一部分為圖中每一個頂點及與該頂點相關(guān)聯(lián)的第一條邊或弧，可以這樣定義：

class VertexAdjacencyList(object):
    """
    圖的一個頂點
    """
    def __init__(self, data):
        self.data = data
        # 與該頂點相連的第一條邊FirstArc
        self.FirstArc = None

使用data域來存儲圖中的每一個頂點，FirstArc域來存儲與該頂點相關(guān)聯(lián)的第一條弧或邊，通常情況下指向第二部分單鏈表的第一個結(jié)點。

第二部分為用一個結(jié)點來存儲圖中的每一條邊或弧，該結(jié)點由adjacent域、info域和NextArc域組成，這些結(jié)點形成了單鏈表。這部分結(jié)點可以這樣定義：

class ArcAdjacencyList(object):
    """
    圖的一個邊(弧)
    """
    def __init__(self, adjacent):
        # 鄰接點或弧頭, 與該頂點相連的另一頂點的index
        self.adjacent = adjacent
        self.info = None
        # 與該邊(弧)依附于相同頂點的下一條邊(弧)NextArc
        self.NextArc = None

根據(jù)上面圖的鄰接表可以這樣定義：

class GraphAdjacencyList(object):
    """
    圖的鄰接表
    """
    def __init__(self, kind):
        # 圖的類型: 無向圖, 有向圖, 無向網(wǎng), 有向網(wǎng)
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 鄰接表
        self.vertices = []
        # 當(dāng)前頂點數(shù)
        self.vexnum = 0
        # 當(dāng)前邊(弧)數(shù)
        self.arcnum = 0

無向圖及其鄰接表：

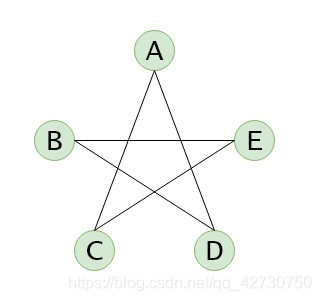
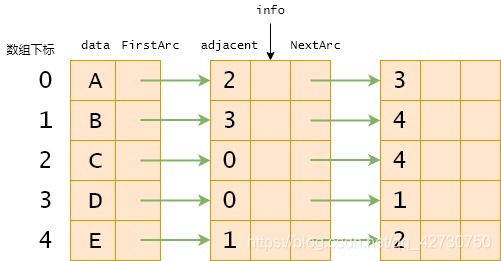
有向網(wǎng)及其鄰接表、逆鄰接表：

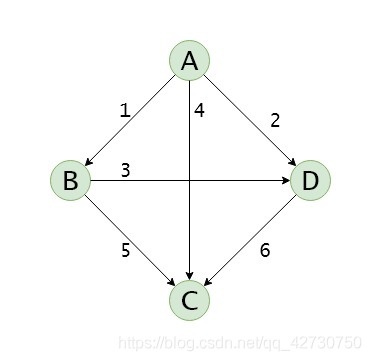
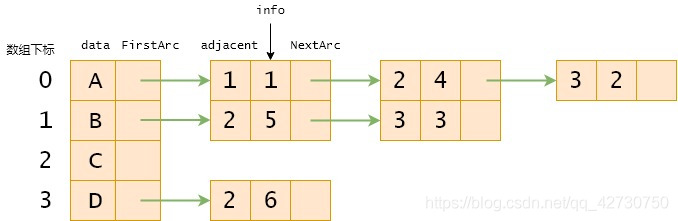
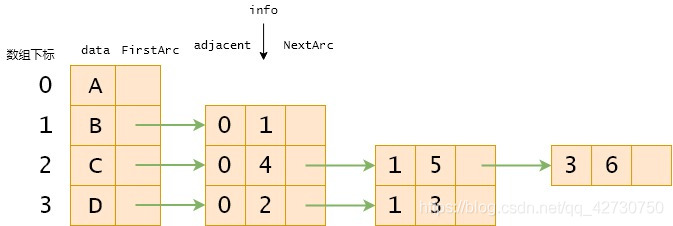
鄰接表的特點如下：

(1) 由于存儲邊或弧通過不同的連接順序會形成不同的單鏈表，所以圖的鄰接表不是唯一的；

(2) 對于具有 e e e條邊的無向圖，使用鄰接表存儲時需要 2 e 2e 2e個結(jié)點來存儲圖的邊，而對于具有 e e e條弧的有向圖，使用鄰接表存儲時需要 e e e個結(jié)點來存儲圖的弧；

(3) 對于具有 n n n個頂點 e e e條邊或弧的稀疏圖而言，若采用鄰接矩陣存儲，則需要 n 2 n^2 n2個存儲空間來存儲圖的邊或弧，而采用鄰接表存儲時，則至多需要 2 e 2e 2e個結(jié)點存儲圖的邊或弧，所以稀疏圖的存儲使用鄰接表會更節(jié)省空間；

(4) 對于無向圖，頂點的度等于該頂點對應(yīng)的單鏈表中結(jié)點的總數(shù)目；

(5) 對于有向圖，若某一頂點在數(shù)組中的下標(biāo)為 i i i，則該頂點的出度為該頂點對應(yīng)的單鏈表中結(jié)點的總數(shù)目，入度為鄰接表中adjacent域內(nèi)值為 i i i的結(jié)點的總數(shù)目。
在使用鄰接表存儲圖時，計算圖中的某一頂點的出度很容易，但是在計算其入度時，最壞的情況需要遍歷整個鄰接表。因此，有時為了方便計算頂點的入度，可以為該圖建立一個逆鄰接表。

在建立鄰接表或逆鄰接表時，如輸入的頂點信息為頂點的編號，則建立鄰接表或逆鄰接表的時間復(fù)雜度為 O ( n + e ) O(n+e) O(n+e)，否則，需要通過查找才能確定頂點在圖中的位置，對應(yīng)的時間復(fù)雜度為 O ( n e ) O(ne) O(ne)。

4.3 十字鏈表

用于有向圖

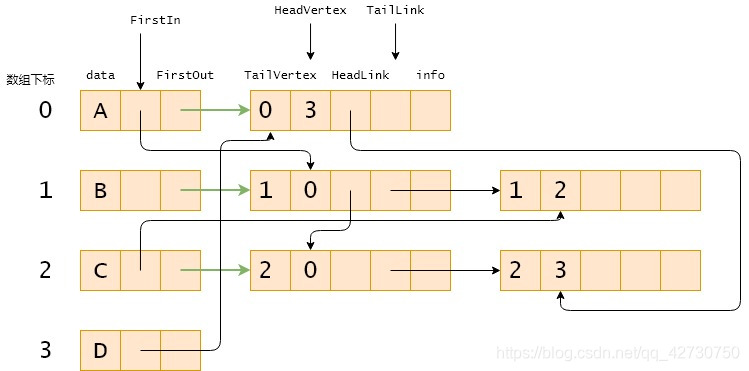
十字鏈表通常用于有向圖，可以將它看成鄰接表和逆鄰接表的結(jié)合。同樣分為兩個部分，即頂點結(jié)點部分和弧部分，通常將頂結(jié)點存儲在數(shù)組中，弧結(jié)點存儲在單鏈表中。

頂點結(jié)點包含data域、FirstIn域和FirstOut域，其中data域存儲頂點的值，FirstIn域指向以當(dāng)前頂點為弧頭的第

一條弧和FirstOut域指向以當(dāng)前頂點為弧尾的第一條弧。
弧結(jié)點包含TailVertex域、HeadVertex域、HeadLink域、TailLink域和info域，其中TailVertex域存儲當(dāng)前弧的弧尾在數(shù)組中的下標(biāo)，HeadVertex域存儲當(dāng)前弧的弧頭在數(shù)組中的下標(biāo)，HeadLink域指向與當(dāng)前弧有相同弧頭的下一條弧，TailLink域指向與當(dāng)前弧有相同弧尾的下一條弧，info域存儲當(dāng)前弧的其他信息。

頂點結(jié)點定義如下：

class VertexOrthogonalList(object):
    """
    有向圖的一個頂點
    """
    def __init__(self, data):
        self.data = data
        # 以該頂點為弧頭的第一條弧FirstIn
        self.FirstIn= None
        # 以該頂點為弧尾的第一條弧FirstOut
        self.FirstOut= None

弧結(jié)點定義如下：

class ArcOrthogonalList(object):
    """
    有向圖的一條弧
    """
    def __init__(self):
        # 當(dāng)前弧中弧頭在數(shù)組中的下標(biāo)HeadVertex
        self.HeadVertex = None
        # 當(dāng)前弧中弧尾在數(shù)組中的下標(biāo)TailVertex
        self.TailVertex = None
        # 與當(dāng)前弧有相同弧頭的下一條弧HeadLink
        self.HeadLink = None
        # 與當(dāng)前弧有相同弧尾的下一條弧TailLink
        self.TailLink = None
        self.info = None

十字鏈表表示的有向圖定義如下：

class GraphOrthogonalList(object):
    """
    有向圖的十字鏈表
    """
    def __init__(self):
        # 十字鏈表
        self.vertices = []
        # 當(dāng)前頂點數(shù)
        self.vexnum = 0
        # 當(dāng)前邊(弧)數(shù)
        self.arcnum = 0

有向圖及其十字鏈表：

4.4 鄰接多重表

用于無向圖

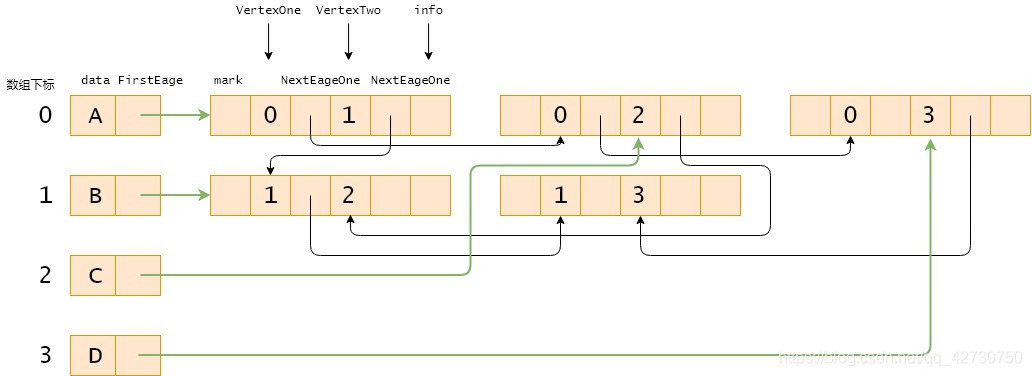
在使用鄰接表存儲無向圖時，圖的每一條邊都對應(yīng)兩個結(jié)點，由于這兩個結(jié)點屬于兩個不同的鄰接表，所以在進行刪除操作時需要對鄰接表的兩條單鏈表進行操作，比較麻煩，所有引出了鄰接多重表。鄰接多重表同樣分為兩個部分，即頂點結(jié)點和邊結(jié)點，通常將頂點結(jié)點存儲在數(shù)組中，邊結(jié)點存儲在單鏈表中。

頂點結(jié)點包含data域和FirstEdge域，其中data域存儲頂點的值，FirstEdge域指向與當(dāng)前頂點相關(guān)聯(lián)的第一條邊。

邊結(jié)點包含mark域、VertexOne域、NextEdgeOne域、VertexTwo域、NextEdgeTwo域和info域，其中mark域用于標(biāo)記當(dāng)前是否被訪問，VertexOne域和VertexTwo域分別存儲當(dāng)前邊的兩個頂點在數(shù)組中的下標(biāo)，NextEdgeOne域指向與VertexOne域?qū)?yīng)的頂點相關(guān)聯(lián)的下一條邊，NextEdgeTwo域指向與VertexTwo域?qū)?yīng)的頂點相關(guān)聯(lián)的下一條邊，info域存儲當(dāng)前邊的其他信息。

頂點結(jié)點定義如下：

class VertexAdjacencyMultitable(object):
    """
    無向圖的一個頂點
    """
    def __init__(self, data):
        self.data = data
        # 與該頂點相連的第一條邊FirstEdge
        self.FirstEdge = None

邊結(jié)點定義如下：

class Edge(object):
    """
    無向圖的鄰接多重表
    """
    def __init__(self):
        # 用來標(biāo)記當(dāng)前邊是否已被訪問過
        self.mark = None
        # 該邊的兩個頂點在數(shù)組中的下標(biāo)
        self.VertexOne = None
        self.VertexTwo = None
        # 與VertexOne對應(yīng)的頂點相連的下一條邊NextEdgeOne
        self.NextEdgeOne = None
        # 與VertexTwo對應(yīng)的頂點相連的下一條邊NextEdgeTwo
        self.NextEdgeTwo = None
        self.info = None

多重鄰接表表示的圖定義如下：

class GraphAdjacencyMultitable(object):
    """
    無向圖的鄰接多重表
    """
    def __init__(self):
        self.vertices = []
        self.vertexnum = 0
        self.edgenum = 0

無向圖及其鄰接多重鏈表：

到此這篇關(guān)于P-ython數(shù)據(jù)結(jié)構(gòu)之圖的存儲結(jié)構(gòu)詳解的文章就介紹到這了,更多相關(guān)P-ython圖的存儲結(jié)構(gòu)內(nèi)容請搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持腳本之家！